import pymc as pm
import numpy as np
import arviz as az
import pandas as pd
import pytensor.tensor.subtensor as st
from itertools import combinations

9. Simvastatin*

This one is about factorial designs (2-way ANOVA) with sum-to-zero and corner constraints.

Adapted from Unit 7: simvastatin.odc.

Data can be found here.

In a quantitative physiology lab II at Georgia Tech, students were asked to find a therapeutic model to test on MC3T3-E1 cell line to enhance osteoblastic growth. The students found a drug called Simvastatin, a cholesterol lowering drug to test on these cells. Using a control and three different concentrations, \(10^{-9}\), \(10^{-8}\) and \(10^{-7}\) M, cells were treated with the drug. These cells were plated on four, 24 well plates with each well plate having a different treatment. To test for osteoblastic differentiation an assay, pNPP, was used to test for alkaline phosphatase activity. The higher the alkaline phosphatase activity the better the cells are differentiating, and become more bone like. This assay was performed 6 times total within 11 days. Each time the assay was performed, four wells from each plate were used.

Note

We can now implement the sum-to-zero (STZ) constraints in PyMC with the pm.ZeroSumNormal class. Previously, we were doing something similar to the corner constraint approach, below, for STZ constraints.

data = pd.read_csv("../data/simvastatin_data.tsv", sep="\t")
data.head(3)

	apa	conc	time
0	0.062	1	1
1	0.517	1	1
2	0.261	1	1

# set up alternate coordinates, the ID3 or clusters column
conc_idx, conc = pd.factorize(data["conc"])
time_idx, time = pd.factorize(data["time"])
coords = {"conc": conc, "time": time, "id": data.index}

conc_idx, time_idx, coords

(array([0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 0, 0, 0, 0, 1, 1,
        1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2,
        3, 3, 3, 3, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 0, 0,
        0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 0, 0, 0, 0, 1, 1, 1, 1,
        2, 2, 2, 2, 3, 3, 3, 3]),
 array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4,
        4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5,
        5, 5, 5, 5, 5, 5, 5, 5]),
 {'conc': Index([1, 2, 3, 4], dtype='int64'),
  'time': Index([1, 2, 3, 4, 5, 6], dtype='int64'),
  'id': RangeIndex(start=0, stop=96, step=1)})

Model 1 with sum-to-zero constraints

def contrasts(var, index):
    """Calculate differences between levels with names like "alpha[low] - alpha[high]".

    var: pytensor.tensor.var.TensorVariable
    index: pandas.Index
    """
    name = var.name
    for i, j in combinations(range(index.size), 2):
        a, b = index[i], index[j]
        pm.Deterministic(f"{name}[{a}] - {name}[{b}]", var[i] - var[j])


with pm.Model(coords=coords) as m:
    apa_data = pm.Data("apa_data", data.apa.to_numpy())
    time_idx_data = pm.Data("time_idx_data", time_idx, dims="id")
    conc_idx_data = pm.Data("conc_idx_data", conc_idx, dims="id")

    mu0 = pm.Normal("mu0", 0, sigma=10)
    alpha = pm.ZeroSumNormal("alpha", sigma=10, dims="conc")
    beta = pm.ZeroSumNormal("beta", sigma=10, dims="time")
    alphabeta = pm.ZeroSumNormal(
        "alphabeta", sigma=10, dims=("conc", "time"), n_zerosum_axes=2
    )

    sigma = pm.Exponential("sigma", 0.05)

    mu = (
        mu0
        + alpha[conc_idx_data]
        + beta[time_idx_data]
        + alphabeta[conc_idx_data, time_idx_data]
    )
    pm.Normal("apa", mu, sigma=sigma, observed=apa_data, dims="id")

    # calculate differences between levels (except interaction term)
    contrasts(alpha, coords["conc"])
    contrasts(beta, coords["time"])

    trace = pm.sample(2000)

Show code cell output Hide code cell output

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu0, alpha, beta, alphabeta, sigma]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 2 seconds.

az.summary(trace)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu0	0.239	0.025	0.192	0.284	0.000	0.000	16025.0	6047.0	1.0
alpha[1]	0.050	0.043	-0.029	0.130	0.000	0.000	16137.0	5345.0	1.0
alpha[2]	0.068	0.044	-0.015	0.151	0.000	0.000	17739.0	6112.0	1.0
alpha[3]	-0.075	0.043	-0.155	0.008	0.000	0.000	15878.0	5571.0	1.0
alpha[4]	-0.042	0.043	-0.122	0.040	0.000	0.000	16277.0	6767.0	1.0
beta[1]	0.046	0.057	-0.064	0.151	0.000	0.001	17607.0	5500.0	1.0
beta[2]	-0.150	0.056	-0.255	-0.043	0.000	0.000	16229.0	5287.0	1.0
beta[3]	-0.017	0.057	-0.124	0.089	0.000	0.001	15903.0	5838.0	1.0
beta[4]	0.231	0.056	0.127	0.338	0.000	0.000	20296.0	6065.0	1.0
beta[5]	-0.023	0.056	-0.130	0.080	0.000	0.001	17988.0	5377.0	1.0
beta[6]	-0.086	0.056	-0.191	0.020	0.000	0.000	16977.0	6607.0	1.0
alphabeta[1, 1]	-0.087	0.099	-0.282	0.089	0.001	0.001	18737.0	5888.0	1.0
alphabeta[1, 2]	-0.081	0.099	-0.279	0.095	0.001	0.001	17551.0	5878.0	1.0
alphabeta[1, 3]	-0.210	0.096	-0.390	-0.026	0.001	0.001	19321.0	5910.0	1.0
alphabeta[1, 4]	0.501	0.098	0.321	0.690	0.001	0.001	16675.0	5458.0	1.0
alphabeta[1, 5]	-0.021	0.098	-0.202	0.166	0.001	0.001	18033.0	6209.0	1.0
alphabeta[1, 6]	-0.102	0.095	-0.284	0.076	0.001	0.001	17272.0	5672.0	1.0
alphabeta[2, 1]	0.150	0.097	-0.041	0.324	0.001	0.001	18286.0	6128.0	1.0
alphabeta[2, 2]	-0.100	0.099	-0.277	0.098	0.001	0.001	19841.0	5447.0	1.0
alphabeta[2, 3]	0.354	0.099	0.171	0.542	0.001	0.001	18317.0	6005.0	1.0
alphabeta[2, 4]	-0.176	0.099	-0.359	0.012	0.001	0.001	15986.0	6157.0	1.0
alphabeta[2, 5]	-0.186	0.097	-0.371	-0.007	0.001	0.001	18866.0	5949.0	1.0
alphabeta[2, 6]	-0.041	0.098	-0.223	0.147	0.001	0.001	16520.0	5735.0	1.0
alphabeta[3, 1]	-0.044	0.098	-0.221	0.147	0.001	0.001	15690.0	6344.0	1.0
alphabeta[3, 2]	0.056	0.097	-0.135	0.230	0.001	0.001	16679.0	5610.0	1.0
alphabeta[3, 3]	-0.045	0.097	-0.231	0.135	0.001	0.001	16829.0	6033.0	1.0
alphabeta[3, 4]	-0.139	0.100	-0.321	0.052	0.001	0.001	17108.0	5830.0	1.0
alphabeta[3, 5]	0.159	0.098	-0.032	0.342	0.001	0.001	17604.0	6188.0	1.0
alphabeta[3, 6]	0.013	0.097	-0.167	0.195	0.001	0.001	18881.0	6015.0	1.0
alphabeta[4, 1]	-0.020	0.097	-0.198	0.164	0.001	0.001	16763.0	6193.0	1.0
alphabeta[4, 2]	0.125	0.098	-0.056	0.310	0.001	0.001	19270.0	6187.0	1.0
alphabeta[4, 3]	-0.099	0.098	-0.278	0.086	0.001	0.001	18312.0	5739.0	1.0
alphabeta[4, 4]	-0.186	0.096	-0.370	-0.009	0.001	0.001	18164.0	5899.0	1.0
alphabeta[4, 5]	0.048	0.098	-0.137	0.231	0.001	0.001	16290.0	5796.0	1.0
alphabeta[4, 6]	0.131	0.097	-0.046	0.317	0.001	0.001	19710.0	5744.0	1.0
sigma	0.245	0.021	0.206	0.285	0.000	0.000	7177.0	6309.0	1.0
alpha[1] - alpha[2]	-0.019	0.071	-0.153	0.113	0.001	0.001	17208.0	6121.0	1.0
alpha[1] - alpha[3]	0.125	0.070	-0.006	0.255	0.001	0.000	16185.0	5960.0	1.0
alpha[1] - alpha[4]	0.092	0.070	-0.035	0.229	0.001	0.001	15963.0	5886.0	1.0
alpha[2] - alpha[3]	0.143	0.071	0.010	0.277	0.001	0.000	16554.0	5525.0	1.0
alpha[2] - alpha[4]	0.111	0.071	-0.022	0.246	0.001	0.000	17508.0	6694.0	1.0
alpha[3] - alpha[4]	-0.033	0.071	-0.165	0.102	0.001	0.001	16158.0	6125.0	1.0
beta[1] - beta[2]	0.196	0.089	0.039	0.371	0.001	0.001	15356.0	5501.0	1.0
beta[1] - beta[3]	0.064	0.090	-0.101	0.235	0.001	0.001	17456.0	6107.0	1.0
beta[1] - beta[4]	-0.184	0.087	-0.344	-0.018	0.001	0.001	18429.0	5783.0	1.0
beta[1] - beta[5]	0.069	0.086	-0.097	0.227	0.001	0.001	18081.0	5315.0	1.0
beta[1] - beta[6]	0.132	0.088	-0.034	0.298	0.001	0.001	17547.0	6326.0	1.0
beta[2] - beta[3]	-0.133	0.087	-0.295	0.031	0.001	0.001	16051.0	6060.0	1.0
beta[2] - beta[4]	-0.381	0.088	-0.543	-0.214	0.001	0.000	20287.0	5947.0	1.0
beta[2] - beta[5]	-0.128	0.087	-0.294	0.030	0.001	0.001	17175.0	5327.0	1.0
beta[2] - beta[6]	-0.064	0.086	-0.227	0.093	0.001	0.001	16477.0	5940.0	1.0
beta[3] - beta[4]	-0.248	0.087	-0.408	-0.087	0.001	0.001	17316.0	6573.0	1.0
beta[3] - beta[5]	0.005	0.088	-0.160	0.173	0.001	0.001	16760.0	6046.0	1.0
beta[3] - beta[6]	0.069	0.087	-0.099	0.229	0.001	0.001	15885.0	5729.0	1.0
beta[4] - beta[5]	0.253	0.087	0.088	0.415	0.001	0.001	19013.0	5946.0	1.0
beta[4] - beta[6]	0.317	0.088	0.148	0.480	0.001	0.001	18063.0	5965.0	1.0
beta[5] - beta[6]	0.063	0.087	-0.092	0.231	0.001	0.001	17985.0	5835.0	1.0

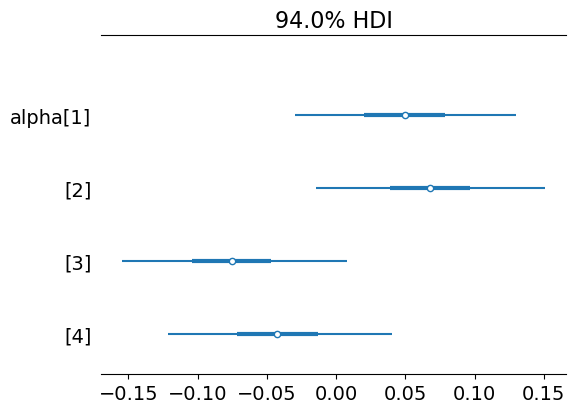
az.plot_forest(trace, var_names=["alpha"], combined=True)

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

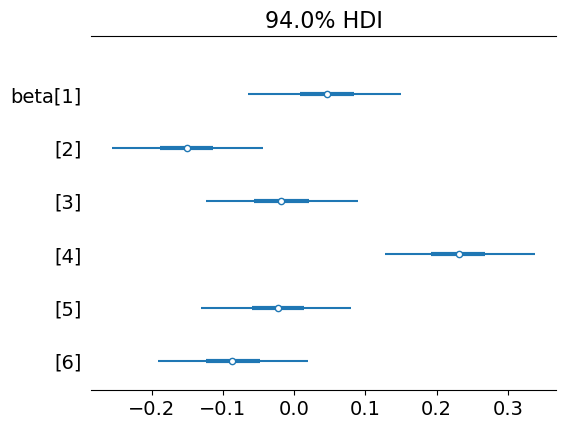
az.plot_forest(trace, var_names=["beta"], combined=True)

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

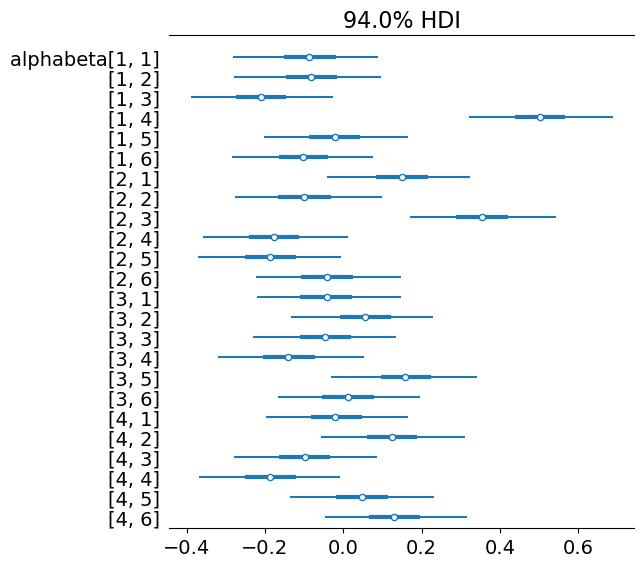
az.plot_forest(trace, var_names=["alphabeta"], combined=True)

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

Model 2 with corner constraints

with pm.Model(coords=coords) as m:
    apa_data = pm.Data("apa_data", data.apa.to_numpy())
    time_idx_data = pm.Data("time_idx_data", time_idx, dims="id")
    conc_idx_data = pm.Data("conc_idx_data", conc_idx, dims="id")

    mu0 = pm.Normal("mu0", 0, tau=0.0001)
    _alpha = pm.Normal("_alpha", 0, tau=0.0001, dims="conc")
    _beta = pm.Normal("_beta", 0, tau=0.0001, dims="time")
    _alphabeta = pm.Normal("_alphabeta", 0, tau=0.0001, dims=("conc", "time"))
    tau = pm.Gamma("tau", 0.001, 0.001)
    sigma = pm.Deterministic("sigma", 1 / tau**0.5)

    # corner constraints: sets the first element of a dimension to zero
    alpha = pm.Deterministic("alpha", st.set_subtensor(_alpha[0], 0), dims="conc")
    beta = pm.Deterministic("beta", st.set_subtensor(_beta[0], 0), dims="time")
    _alphabeta = st.set_subtensor(_alphabeta[:, 0], 0)
    alphabeta = pm.Deterministic(
        "alphabeta",
        st.set_subtensor(_alphabeta[0, :], 0),
        dims=("conc", "time"),
    )

    mu = (
        mu0
        + alpha[conc_idx_data]
        + beta[time_idx_data]
        + alphabeta[conc_idx_data, time_idx_data]
    )
    pm.Normal("apa", mu, tau=tau, observed=apa_data, dims="id")

    contrasts(alpha, coords["conc"])
    contrasts(beta, coords["time"])

    trace = pm.sample(2000)

Show code cell output Hide code cell output

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu0, _alpha, _beta, _alphabeta, tau]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 7 seconds.

az.summary(trace, var_names="~_", filter_vars="like", kind="stats")

	mean	sd	hdi_3%	hdi_97%
mu0	0.246	0.125	0.009	0.478
tau	17.175	2.895	11.826	22.607
sigma	0.244	0.021	0.206	0.283
alpha[1]	0.000	0.000	0.000	0.000
alpha[2]	0.255	0.174	-0.066	0.587
alpha[3]	-0.080	0.177	-0.419	0.250
alpha[4]	-0.023	0.176	-0.359	0.304
beta[1]	0.000	0.000	0.000	0.000
beta[2]	-0.188	0.174	-0.503	0.154
beta[3]	-0.187	0.176	-0.508	0.156
beta[4]	0.773	0.177	0.436	1.095
beta[5]	-0.001	0.177	-0.323	0.337
beta[6]	-0.145	0.177	-0.473	0.191
alphabeta[1, 1]	0.000	0.000	0.000	0.000
alphabeta[1, 2]	0.000	0.000	0.000	0.000
alphabeta[1, 3]	0.000	0.000	0.000	0.000
alphabeta[1, 4]	0.000	0.000	0.000	0.000
alphabeta[1, 5]	0.000	0.000	0.000	0.000
alphabeta[1, 6]	0.000	0.000	0.000	0.000
alphabeta[2, 1]	0.000	0.000	0.000	0.000
alphabeta[2, 2]	-0.258	0.246	-0.721	0.209
alphabeta[2, 3]	0.329	0.248	-0.169	0.779
alphabeta[2, 4]	-0.909	0.245	-1.346	-0.428
alphabeta[2, 5]	-0.400	0.249	-0.885	0.063
alphabeta[2, 6]	-0.176	0.246	-0.659	0.269
alphabeta[3, 1]	0.000	0.000	0.000	0.000
alphabeta[3, 2]	0.091	0.247	-0.407	0.519
alphabeta[3, 3]	0.121	0.248	-0.358	0.569
alphabeta[3, 4]	-0.684	0.249	-1.135	-0.212
alphabeta[3, 5]	0.133	0.249	-0.332	0.608
alphabeta[3, 6]	0.070	0.252	-0.411	0.541
alphabeta[4, 1]	0.000	0.000	0.000	0.000
alphabeta[4, 2]	0.137	0.247	-0.313	0.617
alphabeta[4, 3]	0.045	0.246	-0.407	0.506
alphabeta[4, 4]	-0.757	0.248	-1.243	-0.303
alphabeta[4, 5]	0.000	0.250	-0.491	0.445
alphabeta[4, 6]	0.164	0.249	-0.287	0.650
alpha[1] - alpha[2]	-0.255	0.174	-0.587	0.066
alpha[1] - alpha[3]	0.080	0.177	-0.250	0.419
alpha[1] - alpha[4]	0.023	0.176	-0.304	0.359
alpha[2] - alpha[3]	0.335	0.174	0.014	0.669
alpha[2] - alpha[4]	0.278	0.172	-0.046	0.603
alpha[3] - alpha[4]	-0.057	0.175	-0.387	0.267
beta[1] - beta[2]	0.188	0.174	-0.154	0.503
beta[1] - beta[3]	0.187	0.176	-0.156	0.508
beta[1] - beta[4]	-0.773	0.177	-1.095	-0.436
beta[1] - beta[5]	0.001	0.177	-0.337	0.323
beta[1] - beta[6]	0.145	0.177	-0.191	0.473
beta[2] - beta[3]	-0.001	0.174	-0.340	0.316
beta[2] - beta[4]	-0.961	0.171	-1.293	-0.655
beta[2] - beta[5]	-0.188	0.173	-0.529	0.127
beta[2] - beta[6]	-0.044	0.173	-0.364	0.285
beta[3] - beta[4]	-0.960	0.175	-1.284	-0.627
beta[3] - beta[5]	-0.186	0.174	-0.511	0.140
beta[3] - beta[6]	-0.042	0.176	-0.359	0.297
beta[4] - beta[5]	0.774	0.176	0.444	1.095
beta[4] - beta[6]	0.918	0.175	0.596	1.246
beta[5] - beta[6]	0.144	0.176	-0.184	0.474

%load_ext watermark
%watermark -n -u -v -iv

Last updated: Sun Mar 09 2025

Python implementation: CPython
Python version       : 3.12.7
IPython version      : 8.29.0

pymc    : 5.19.1
numpy   : 1.26.4
pandas  : 2.2.3
arviz   : 0.20.0
pytensor: 2.26.4