import matplotlib.pyplot as plt
import numpy as np
from tqdm.auto import tqdm

7. Metropolis: Normal-Cauchy*

Adapted from Unit 5: norcaumet.m.

For this example, our model is:

\[\begin{split} \begin{align} X \mid \theta &\sim N(\theta, 1) \\ \theta &\sim \text{Cauchy}(0, 1) \end{align} \end{split}\]

We have a single datapoint, \(x=2\). The professor chose a \(N(x, 1)\) proposal. This is not symmetric around the current state of the chain, so it doesn’t satisfy \(q(\theta^\prime| \theta) = q(\theta | \theta^\prime)\) and we must use Metropolis-Hastings.

Original method

Here’s how we set up this problem. Assuming we have \(n\) independent data points, the likelihood is:

\[\begin{split} \begin{align*} L(\theta; X) &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi}} \exp\!\left(-\frac{(x_i-\theta)^2}{2}\right) \\ &\propto \prod_{i=1}^n \exp\!\left(-\frac{(x_i-\theta)^2}{2}\right) \end{align*} \end{split}\]

The Cauchy prior density is:

\[ \pi(\theta) = \frac{1}{\pi (1+\theta^2)} \]

Then our posterior is proportional to:

\[\begin{split} \begin{align*} \pi(\theta \mid X) &\propto L(\theta; X) \, \pi(\theta) \\ &\propto \left[\prod_{i=1}^n \exp\!\left(-\frac{(x_i-\theta)^2}{2}\right)\right] \frac{1}{1+\theta^2} \end{align*} \end{split}\]

When proposing a new value \(\theta'\) from a proposal density \( q(\theta' \mid \theta) \), the acceptance ratio is defined as:

\[ \rho = \frac{\pi(\theta' \mid X)\, q(\theta \mid \theta')}{\pi(\theta \mid X)\, q(\theta' \mid \theta)} \]

Substituting the expression for the posterior, we get:

\[\begin{split} \begin{align*} \rho &= \frac{\left\{\prod_{i=1}^n \exp\!\left(-\frac{(x_i-\theta')^2}{2}\right)\right\} \frac{1}{1+(\theta')^2}\, q(\theta \mid \theta')}{\left\{\prod_{i=1}^n \exp\!\left(-\frac{(x_i-\theta)^2}{2}\right)\right\} \frac{1}{1+\theta^2}\, q(\theta' \mid \theta)} \\ &= \frac{1+\theta^2}{1+(\theta')^2} \, \exp\!\left\{-\frac{1}{2}\sum_{i=1}^n \Bigl[ (x_i-\theta')^2 - (x_i-\theta)^2 \Bigr]\right\}\, \frac{q(\theta \mid \theta')}{q(\theta' \mid \theta)}\\ &= \frac{1+\theta^2}{1+(\theta')^2} \, \exp\!\left\{-\frac{1}{2} \Bigl[ (2-\theta')^2 - (2-\theta)^2 \Bigr]\right\}\, \frac{q(\theta \mid \theta')}{q(\theta' \mid \theta)} \end{align*} \end{split}\]

Now there are a lot of ways to choose the proposal \(q(\cdot)\). In this case, the professor has chosen one that will simplify our acceptance ratio expression quite a bit, \(N(x, 1)\). I’ll also show how a random walk proposal would work later.

For this example, remember \(n=1\) and \(x=2\).

Since the professor chooses an “independence” proposal, the proposal density is independent of the current state:

\[ q(\theta' \mid \theta) = q(\theta') = N(2, 1) \]

\[ q(\theta \mid \theta') = q(\theta) = N(2, 1) \]

The ratio of the proposal densities becomes

\[\begin{split} \begin{align*} \frac{q(\theta \mid \theta')}{q(\theta' \mid \theta)} &= \frac{N(2,1)(\theta)}{N(2,1)(\theta')} \\ &= \frac{\frac{1}{\sqrt{2\pi}} \exp\!\left(-\frac{1}{2}(\theta-2)^2\right)} {\frac{1}{\sqrt{2\pi}} \exp\!\left(-\frac{1}{2}(\theta'-2)^2\right)}\\ &= \exp\!\left\{-\frac{1}{2}\Bigl[(\theta-2)^2 - (\theta'-2)^2\Bigr]\right\}\\ \end{align*} \end{split}\]

Substitute this back into the acceptance ratio:

\[\begin{split} \begin{align} \rho &= \frac{1+\theta^2}{1+(\theta')^2}\, \exp\!\left\{-\frac{1}{2}\Bigl[(2-\theta')^2-(2-\theta)^2\Bigr]\\ -\frac{1}{2}\Bigl[(\theta-2)^2-(\theta'-2)^2\Bigr]\right\} \end{align} \end{split}\]

Use the following fact:

\[ (2-\theta)^2 = (\theta-2)^2 \quad \text{and} \quad (2-\theta')^2 = (\theta'-2)^2 \]

To see that the exponential terms cancel:

\[ -\frac{1}{2}\Bigl[(2-\theta')^2-(2-\theta)^2\Bigr] -\frac{1}{2}\Bigl[(\theta-2)^2-(\theta'-2)^2\Bigr] = 0 \]

This leaves us with a simplified acceptance ratio:

\[ \rho = \frac{1+\theta^2}{1+\theta'^2} \]

That’s all we need to code our sampler.

Warning

I usually pre-generate arrays of random numbers (see theta_prop and unif variables in the below cell) because it’s computationally faster. However, that only works when those numbers don’t depend on the previous step in the sampling loop.

rng = np.random.default_rng(1)

n = 1000000  # observations
burn = 500
theta = 1  # init
thetas = np.zeros(n)
x = 2  # observed

accepted = 0

# generating necessary randoms as arrays is faster
theta_prop = rng.standard_normal(n) + x
unif = rng.uniform(size=n)

for i in tqdm(range(n)):
    r = (1 + theta**2) / (1 + theta_prop[i] ** 2)
    rho = min(r, 1)
    if unif[i] < rho:
        theta = theta_prop[i]
        accepted += 1
    thetas[i] = theta

thetas = thetas[burn:]

print(f"{np.mean(thetas)=:.3f}")
print(f"{np.var(thetas)=:.3f}")
print(f"{accepted/n=:.3f}")

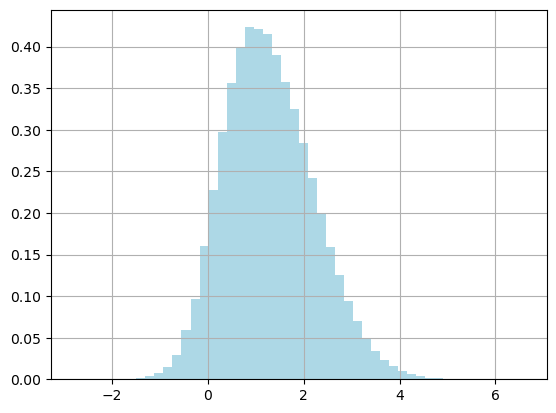
fig, ax = plt.subplots()
ax.grid(True)
plt.hist(thetas, color="lightblue", density=True, bins=50)
plt.show()

np.mean(thetas)=1.283
np.var(thetas)=0.863
accepted/n=0.588

Random-walk proposal

How would we do this with classic Metropolis? We would use a random-walk proposal, centering the proposal at the previous state of the chain at each step.

Notice I can still pregenerate proposal values, because it’s easy to adjust the pregenerated \(N(0, 1)\) values by adding theta, which centers the distribution at the previous state of the chain.

n = 1000000
burn = 500
theta = 1
thetas = np.zeros(n)
x = 2

accepted = 0

theta_prop = rng.standard_normal(n)
unif = rng.uniform(size=n)


def f(x, theta):
    return np.exp(-0.5 * (x - theta) ** 2) / (1 + theta**2)


for i in tqdm(range(n)):
    theta_prop_current = theta_prop[i] + theta

    r = f(x, theta_prop_current) / f(x, theta)
    rho = min(r, 1)

    if unif[i] < rho:
        theta = theta_prop_current
        accepted += 1

    thetas[i] = theta

thetas = thetas[burn:]

print(f"{np.mean(thetas)=:.3f}")
print(f"{np.var(thetas)=:.3f}")
print(f"{accepted/n=:.3f}")

fig, ax = plt.subplots()
ax.grid(True)
plt.hist(thetas, color="lightblue", density=True, bins=50)
plt.show()

np.mean(thetas)=1.283
np.var(thetas)=0.865
accepted/n=0.686

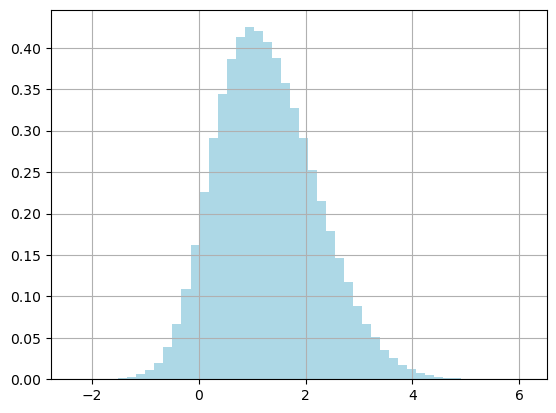
The end results are the same, with a higher acceptance rate! Something to consider: do we always want this behavior from the sampler?

%load_ext watermark
%watermark -n -u -v -iv

Last updated: Thu Feb 13 2025

Python implementation: CPython
Python version       : 3.12.7
IPython version      : 8.29.0

matplotlib: 3.9.2
tqdm      : 4.67.0
numpy     : 1.26.4